Scale-free Control in Platoons

Replacing human drivers with autonomous systems has the potential to make driving safer and more efficient. However even the problem of autonomously keeping the distance between vehicles constant so as to prevent traffic jams and crashes is extremely challenging. In this post we investigate this problem from a control theoretic perspective, and discuss the scale-free solution presented in this paper that I wrote with Kaoru Yamamoto.

The platooning problem

We consider the problem of designing decentralised control laws for platooning vehicles. More specifically we consider how to design a control law that determines how a given car adjusts its throttle input in response to measuring the distances to its neighbours. Such control laws could be used to automate the process of regulating the distance between cars on roads.

This has the potential to make highways safer and more efficient, however designing suitable control laws is a very challenging problem (we are all familiar with the infamous traffic jam). This is in part because the way any given control law affects the platoon depends quite heavily on the number of vehicles in the platoon, as illustrated in the following figures:

In these figures the black lines show how the position of each vehicle in the platoon evolves over time when subject to a disturbance (the red line gives the platoon length in the absence of disturbances). In both figures the same control law is used to regulate the distances between vehicles, the only difference is the number of vehicles. Interestingly the behaviour is significantly more oscillatory in the case with 20 vehicles, though in both cases it would be hoped the behaviour could be improved.

The scale-free control problem

These figures beg the question, ‘can we design the control law so that it works well independently of the number of vehicles?’. That is:

Can we make the design scale-free?

To tackle this problem, we use a simplified model of a platoon that is analogous to a mass chain. In this model, each mass in the chain represents a vehicle.

The impedance \(Z\) (a generalisation of a spring constant) determines how the control law affects the positions of each vehicle when they are subject to disturbances. For simplicity we assume each car has identical mass and implements the same control law.

Our job as the designer is to specify the dynamics of the control law. We therefore need a way to evaluate whether a particular design is good or not. To do so, we use a function \(F_N(Z)\), which quantifies the effectiveness a given control law \(Z\) in a platoon of \(N\) vehicles. The details of the function are not important here, just that ensuring

\[F_N(Z)\leq{}\gamma,\]

where \(\gamma\) is a performance level, guarantees acceptable performance. The specific function we consider is given in the paper, and is closely related to the sensitivity function from classical control.

We are now ready to state the scale-free synthesis problem:

\begin{equation}
\text{Find }Z\text{ such that: }\sup_{N}F_N(Z)\leq{}\gamma.\qquad\qquad(1)
\end{equation}

Solving this problem would yield a \(Z\) that ensured acceptable performance no matter how many vehicles \(N\) were in the platoon. Therefore if we were able to solve such a problem then we could guarantee that our designed control law \(Z\) would work well in platoons of all lengths.

A scale free solution

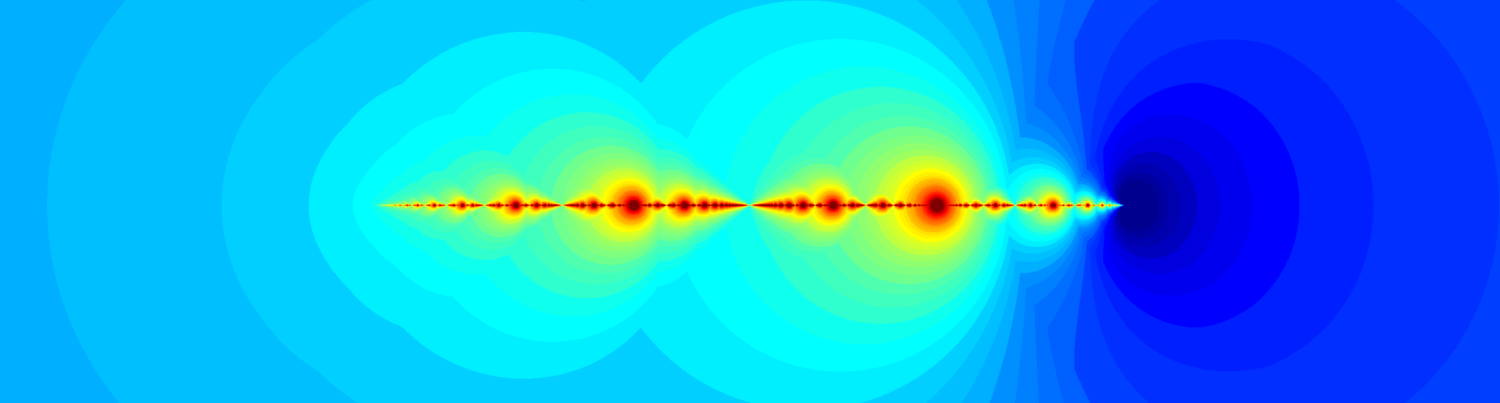
Unfortunately even evaluating the supremum for a given \(Z\), let alone searching for a suitable one, is a very daunting task. We therefore look for further insights by studying the evolution of \(F_N(Z)\) as a function of \(N\). Interestingly it turns out that the theory of complex iterated maps, the theory behind the famous Mandelbrot set, provides the perfect tools for this. In fact, the fractal in the header of this post is generated by considering properties of the iteration \(F_N(Z)\mapsto{}F_{N+1}(Z)\) (the interested reader should refer to Kaoru’s thesis for more details).

The contribution of this paper is to exploit this fact to derive a function \(f(Z)\) with the following key properties:

1. It can be easily evaluated.
2. \(f(Z)\geq{}\sup_{N}F_N(Z)\).

This allows us, at the expense of some conservatism, to replace equation (1) with the following far simpler feasibility problem:

\begin{equation}
\text{Find }Z\text{ such that: }f(Z)\leq{}\gamma.\qquad\qquad(2)
\end{equation}

Critically any guarantees we can obtain from this problem will apply to our scale-free design problem. Tackling equation (2) allowed us to come up with a designs that shows significant improvement. The following figures show the performance achieved in the 20 and 50 vehicle test discussed earlier with a controller designed with respect to (2).