Can Global Behaviours be Controlled Locally?

The premise of decentralised control is to regulate the behaviour of a large interconnected system by designing controllers for the individual components in the network. Its strength is its simplicity, since it requires no complicated or vulnerable communication network to implement the control. In short, if one can solve one’s network control problem using decentralised control, one should. But what types of control problem can be solved using decentralised control?

In this post, which relates to a paper Kaoru Yamamoto and I recently presented at the Conference on Decision and Control, we explore this question in the context of vehicle platooning. We show that while global behaviours are inevitable, their size can be effectively regulated by decentralised controllers.

The emergence of global behaviours

A fascinating test-bed for investigating the potential of decentralised control is the control of vehicle platoons. In this application local behaviours (the distances between the individual cars) can be effectively regulated using decentralised control. However global behaviours (the length of the platoon) seemingly cannot — no matter what the control!

This was the topic of a previous post where it was shown that controllers with scale-free guarantees could be effectively designed using a method based on the theory of complex iterative maps. Nevertheless, while these controllers could regulate the distance between cars very effectively, a global behaviour, while slight, did remain. This behaviour can be seen in the following figure, which shows the trajectories of a platoon of 50 vehicles when the distances between vehicles are being regulated by decentralised controllers.

Although the behaviour of the platoon is well regulated, the overall length of the platoon is oscillating slightly in the presence of disturbances. Of course this figure was generated using a particular controller, and based on this figure it is not clear whether a `better’ design could eliminate this behaviour. The question is then:

Are these oscillations a fundamental consequence of using decentralised control?

We address this question by studying the entries of the transfer function

\[S_N=\left(I+P(s)C(s)L_N\right)^{-1},\]

where

\[L_N  =\begin{bmatrix}1 & -1 & 0 &\cdots&0 \\
-1 & 2 & \ddots{} &\ddots{} &\vdots{} \\
0 & \ddots & \ddots & \ddots&0 \\
\vdots{}&\ddots{}&\ddots{}&\ddots{}&-1\\
0 & \cdots{} &0& -1 & 2\end{bmatrix} \in \mathbb{R}^{N\times N}.\]

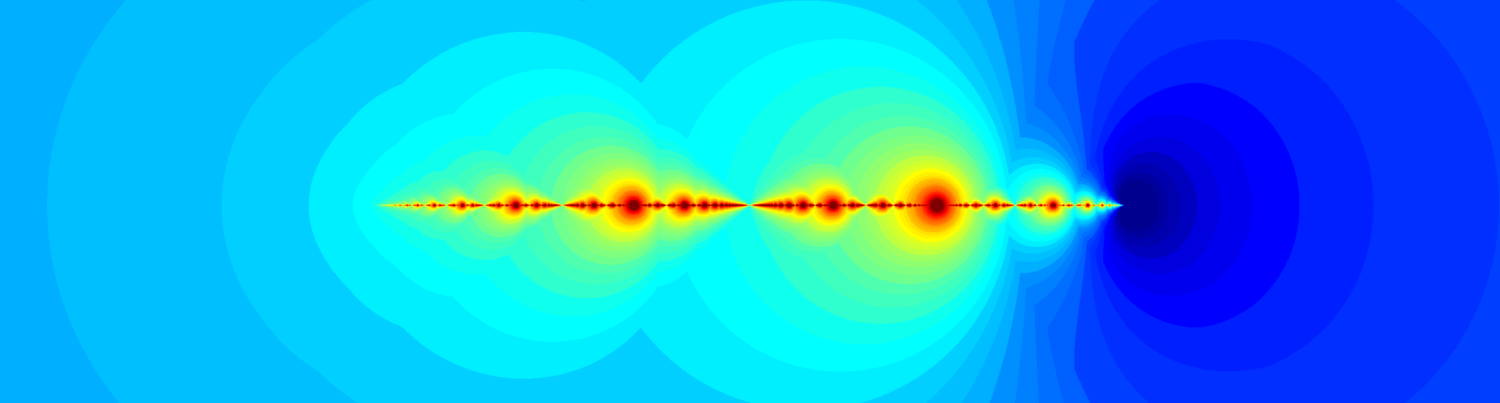
This is the (output) sensitivity function of a platoon of \(N\) vehicles when a bidirectional decentralised control scheme is employed. The transfer function \(P(s)\) describes the car dynamics, and \(C(s)\) those of the controllers. The \((i,j)\)th entry of \(S_N(s)\) determines how a disturbance to the position of the \(j\)th vehicle effects the position of the \(i\)th. The Bode magnitude plots for a selection of entries of this transfer function when \(N=30\) and \[P(s)C(s)=\frac{1}{s^2(0.1s+1)}\frac{2s+1}{0.05s+1}\qquad\qquad(1)\]are shown in the following figure:

We see from this figure that for these particular values of \(P(s)\) and \(C(s)\) the individual entries of \(S_N(s)\) remain quite small. This explains why the distances in between vehicles remain small even in the presence of disturbances.

This figure also has an unexpected feature: the emergence of a peak at low frequencies. This peak appears with the same magnitude and the same frequency in every single entry of \(S_N(s)\). This explains the source of the poorly regulated low frequency long length scale mode in the behaviour of the platoon. Since every entry has a peak of the same height and frequency, on slow time scales disturbances to the positions of any vehicle will have the effect of moving all the vehicles by a similar amount – a low frequency, long length scale behaviour!

Controlling global behaviours

Our main contribution is to give a formula for the height of this peak. In particular, if \(P(s)C(s)\) has a repeated pole at the origin and Laurent series expansion

\[P(s)C(s)=\frac{a_{-2}}{s^2}+\frac{a_{-1}}{s}+\ldots{},\]

then in the limit \(N\rightarrow{}\infty\) the peak height is given by

\[
\frac{4}{\pi{}\left|{a_{-1}\sqrt{a_{-2}}}\right|}.
\]

For example if \(P(s)C(s)\) is given by (1), then since

\[
\frac{1}{s^2(0.1s+1)}\frac{2s+1}{0.05s+1}=\frac{1}{s^2}+\frac{7}{4s}+\cdots{},
\]

this formula shows that the peak height is \(16/7\pi\). This value approximately equals -3 dB, and matches well with the peak height in the figure above. This is a unique feature of the case when \(P(s)C(s)\) has imaginary axis poles of multiplicity 2. If the multiplicity is lower, then the peak will not last for all \(N\) (it may never emerge at all), and if it is higher then \(S_N(s)\) will be unstable if \(N\) is sufficiently large. This shows that the oscillations are inevitable in platoons, since these models always have a repeated pole at the origin.

However we can mitigate this effect by designing a controller that leads to small values of \(a_{-2}\) and \(a_{-1}\). For example if we redesign the controller in (1) such that

\[P(s)C(s)=\frac{1}{s^2(0.1s+1)}\frac{(s+0.05)(s+10)}{(0.01s+1)(0.02s+1)}=\frac{0.5}{s^2}+\frac{9.985}{s}+\ldots{},\]

then the peak height approximately equals -15 dB, which is significantly lower than before. This leads to a pronounced improvement in the regulation of the large scale behaviour of the platoon, as can be clearly seen in the following figure.